摘 要: 分析了渦街流量計的基本原理; 運用可壓縮流體的流體力學方程，對渦街流量計的流場速度進行了計算分析，得到了可壓縮流體中等熵指數(shù) κ 對儀表系數(shù)影響的計算公式，并采用 MATLAB 對公式進行了計算分析，發(fā)現(xiàn)儀表系數(shù)隨流體可膨脹性的加劇而呈現(xiàn)增大的的變化趨勢，且在速度為 50 m/s 時偏差達到 1． 54% ; 非常后，通過實驗測試數(shù)據(jù)及 CFD 仿真對可壓縮流體和不可壓縮流體的儀表系數(shù)進行了研究，研究結果表明，理論計算得到的系數(shù)偏差曲線與實驗測試和仿真得到的系數(shù)偏差曲線變化趨勢一致。

1 引 言

渦街流量計自 20 世紀 60 年代末開始研制至今，已開發(fā)出眾多類型漩渦發(fā)生體及檢測方法的渦街流量計，流體的體積流量與它輸出的頻率信號成正比，量程范圍較寬，結構簡單，維護費低，可用于液體、氣體和蒸汽等不同流體的計量，被廣泛應用于計量和工業(yè)過程控制領域中，但是應該看到，渦街流量計尚屬發(fā)展中的流量計，無論其理論基礎還是實踐經(jīng)驗不盡完善。還有許多工作需要探索、充 實。近年來，國內(nèi)外科研工作者針對渦街流量計開展了大量的研究，并取得了一定成果。

按照卡門渦街理論，渦街流量計旋渦分離的頻率僅與流體工作狀態(tài)下的體積流量成正比，而對被測流 體 溫 度、壓 力、密 度、黏度和組分變化不敏感［8-11］。但在實際測試中，這些參數(shù)的變化會對計量性能造成一定量的影響，但對渦街流量計測量帶來多大的附加誤差的研究報道很少。采用理論計算分析及計算流體力學仿真，對氣體流量測量中，氣體的壓縮性對渦街流量計計量性能的影響進行了分析，并進行了實驗驗證分析。

 2 卡門渦街流量計的基本原理

如圖 1 所示，在測量管道中垂直地插入一非流線型阻流體，也稱旋渦發(fā)生體。隨著流體流動，當管道雷諾數(shù)達到一定值時，在發(fā)生體兩側(cè)就會交替地分離出卡門渦街。旋渦頻率 f 與流經(jīng)發(fā)生體兩側(cè)的平均流速 U1 及被測介質(zhì)來流的平均流速 U 之間的關系可表示為:

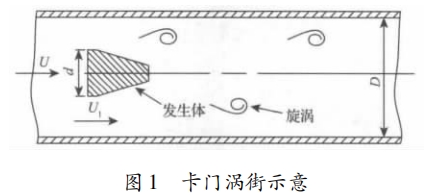
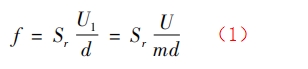
式中: f 為旋渦頻率，Hz; Sr 為斯特勞哈爾數(shù); U1 為發(fā)生體兩側(cè)的平均流速，m/s; d 為發(fā)生體迎流面的寬度，m; U 為被測介質(zhì)來流的平均流速，m/s; m 為旋渦發(fā)生體兩側(cè)弓形面積與管道橫截面面積之比。

由此可得體積流量 qv:

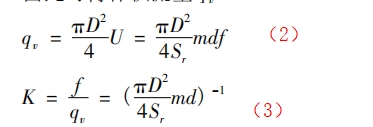
式中: K 為渦街流量計的儀表系數(shù)，1 /m3。從式( 2) 、( 3) 可以看出，對于確定的 D 和 d，流體的體積流量 qv 與旋渦頻率 f 成正比，而 f 只與流速U 和旋渦發(fā)生體的幾何參數(shù)有關，而與被測流體的物性和組分無關，因此可以得出渦街流量計不受流體溫度、壓力、密度、黏度、組分因素影響的結論。 

3 可壓縮性影響的理論分析

流體在渦街流量計流動過程中，對于不可壓縮流體，其流動過程遵循不可壓縮公式的連續(xù)性方程( 4) :A1U = A2U1 ( 4)

式中: A1 為管道橫截面面積，m2 ; A2 為旋渦發(fā)生體兩側(cè)弓形面積 m2 ;由式( 4) 中可以得到:

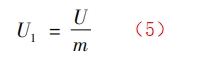
因此可以看出，式( 1) ～ 式( 3) 是基于不可壓縮流體的連續(xù)性方程推導而得到。

但對于可壓縮流體公式( 5) 就不再成立，流動過程遵循可壓縮流體的連續(xù)性方程( 6) 、伯努利方程( 7) 以及等熵過程方程( 8) :

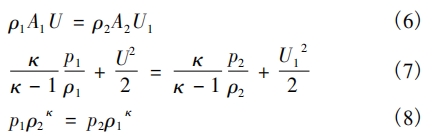
式中: κ 為可壓縮流體的等熵指數(shù); p1 和 p2 管道截面處和發(fā)生體兩側(cè)處的壓力; ρ1 和ρ2 為管道截面處和發(fā)生體兩側(cè)處的介質(zhì)的密度。

由式( 6) ～ 式( 8) 得: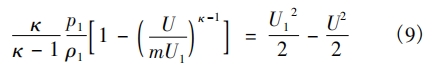

式( 9) 描述了可壓縮流體測試條件下，U、U1、m三者的關系，與描述不可壓縮流體三者之間的關系公式( 5) 不同，三者的關系還和等熵指數(shù)、管道截面處壓力p1、管道截面處流質(zhì)的密度ρ1 有關。以空氣為介質(zhì)檢測渦街流量計時，在一定壓力范圍內(nèi)，空氣看作理想氣體，在溫度不變的情況下，p1 /ρ1 為定值，根據(jù)式( 9) 可以得到，在恒溫的條件下，壓力對儀表系數(shù)沒有影響，僅與等熵指數(shù) κ 有關。

由于 m 為旋渦發(fā)生體兩側(cè)弓形面積與管道橫截面面積之比，按照渦街流量的通用設計［13-14］，對三角柱形發(fā)生體，在 d /D = 0． 28 時漩渦發(fā)生的頻率信號非常強，取 d /D = 0． 28，根據(jù) m 的計算式( 10) 得:

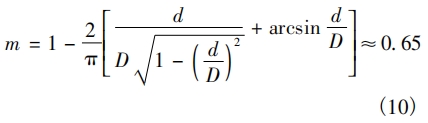
在實驗過程中，以空氣作為可壓縮流體進行測試，按照實際實驗條件和測試用渦街流量計的參數(shù)，各 參 數(shù) 為 壓 力 p1 為 絕 壓 0． 1 MPa，溫 度 為20℃，查空氣性質(zhì)表得 κ = 1． 4［15］，此時空氣的密度ρ1 為 1． 22 kg /m3。

將上述參數(shù)代入式( 9) 中，采用 MATLAB 對式( 9) 進行分析計算，得到可壓縮流體發(fā)生體兩側(cè)平均流速 U1 隨管道平均流速 U 變化的數(shù)值，按照不可壓縮流體計算式( 5) 得到發(fā)生體兩側(cè)平均流速U1 '，計算得到可壓縮性引起的計量偏差 E 為:

不同管道平均流速 U 下，計算分析得到的計量偏差 E 數(shù)據(jù)如表 1 所示。

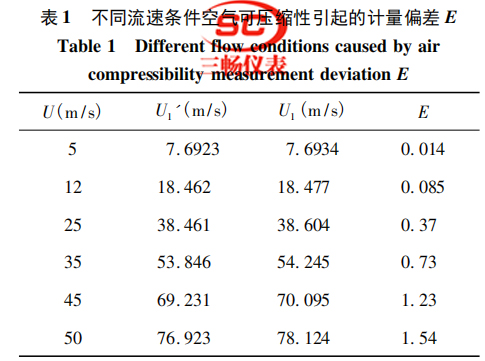
表1 描述了空氣的可壓縮性帶來的計量偏差，可以看出隨可壓縮氣體管道平均流速的增大，將 U1 代入式( 1) 中，渦街流量計產(chǎn)生頻率f增大，導致

式( 3) 中儀表系數(shù) K 值增大，隨流速的增大可膨脹性引起的計量偏差會逐漸增大。 

4 試驗測試分析

選取 DN100 及 DN50 渦街流量計各 1 臺，分別在水流量計量標準裝置及負壓法音速噴嘴裝置中測試儀表系數(shù)，測試數(shù)據(jù)分別如圖 2 和圖 3 所示。

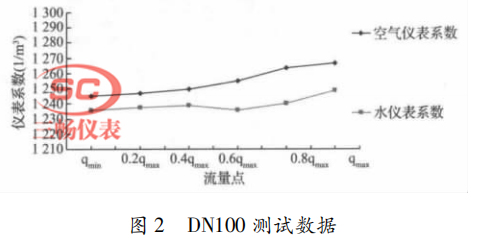
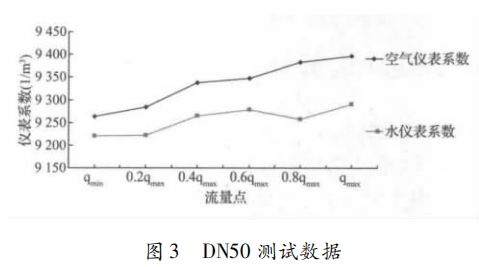
由實驗數(shù)據(jù)可以看出在空氣介質(zhì)中測試的儀表系數(shù)比在水中測試的儀表系數(shù)偏大，這與空氣為可壓縮流體有關，空氣中測試得到的儀表系數(shù)隨流量的增大逐漸增大，與理論分析相符。

在實際空氣介質(zhì)測量時，空氣的上限流速一般為 50 m/s，根據(jù)表 1 數(shù)據(jù)分析，在上限引起的偏差為 1． 54% ，按照國家檢定規(guī)程《JJG1029 － 2007 渦街流量計檢定規(guī)程》中儀表系數(shù)的計算方法［16］，可對整體儀表系數(shù)造成 0． 77% 的偏差，可壓縮氣體對渦街流量計實驗結果與理論分析趨勢基本相符。

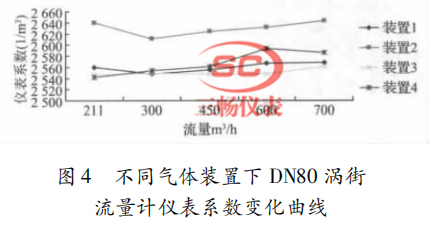
為了避免出現(xiàn)由于計量標準裝置的計量偏差引起的儀表系數(shù)變化，分析了由遼寧省計量科學研究院陳梅、韓聰?shù)热税l(fā)表的《渦街流量計在不同的空氣流量標準裝置上測量結果的比較》文章中的數(shù)據(jù)［17］，在該文章中由遼寧省計量科學研究院組織了 5 臺氣體流量標準裝置進行了比對，標準表選用了 2 臺 DN80 的渦街流量計，2 臺流量計變化曲線基本相似，選取其中 1 臺的測試數(shù)據(jù)曲線圖，如 圖 4 所示。共有 4 臺標準裝置的測試曲線，另外 1臺裝置明顯存有偏差，為無效數(shù)據(jù)，通過 4 臺裝置的數(shù)據(jù)也可以看出隨流量增大，儀表系數(shù) K 值剔除非常好點外，存在隨流量增大而逐漸增大的趨勢。

5、CFD 仿真分析（篇幅原因，省略）

6、結 論

通過理論計算分析，實驗數(shù)據(jù)驗證及計算流體力學仿真可得到如下結論: 

1) 渦街流量計在氣體流量計量中，可壓縮氣體的可壓縮性會對儀表系數(shù)造成偏差，偏差與等熵指數(shù)、入口處的壓力與密度比值等參數(shù)有關。 

2) 可壓縮性引起的儀表系數(shù)偏差，可通過計算分析其影響偏差的大小，分析顯示隨流量的增大，該偏差也逐漸增大，可通過計算進行儀表系數(shù)的補償。

3) 以空氣為介質(zhì)檢測渦街流量計時，在一定壓力范圍內(nèi)，在恒溫的條件下，壓力與密度對儀表系數(shù)沒有影響，僅與等熵指數(shù)有關。

4) 以水和其他不可壓縮流量計作為檢測介質(zhì)時由于儀表系數(shù)不受可壓縮性的影響，儀表系數(shù)偏小，并且其儀表系數(shù)的線性度要好于可壓縮流體，在液體計量中精度要高于氣體的計量精度。

影響渦街流量計的儀表系數(shù)有很多因素，實驗數(shù)據(jù)是總體因素的影響，有可能存在其他方面的影響，與理論計算分析不盡吻合，還需進一步深入分析其他因素帶來影響。